Ana Lúcia Rodrigues¹
Carla Franciele Höring²
Brian A. Ribeiro de Melo³
Num recente artigo intitulado As pandemias deprimem a economia, as intervenções de saúde pública não: evidências da gripe de 1918, que analisa a gripe espanhola em 43 cidades dos EUA, os autores concluíram que apesar dos custos econômicos substanciais, “as cidades que intervieram mais cedo e de forma mais agressiva não só não apresentaram desempenho econômico pior como se recuperaram e voltaram a crescer mais rapidamente após o término da pandemia”. Isso significa que as intervenções não farmacêuticas, como o distanciamento social, naquele momento promoveram a redução da mortalidade e, ao mesmo tempo, apresentaram “méritos econômicos”. Este é o nosso pressuposto em defesa das medidas de isolamento social para Maringá, pois em coro com a Congregação da Faculdade de Saúde Pública da USP, concordamos que “não há contradição entre proteção da economia e proteção da saúde pública”, o que demanda programas e investimentos públicos do Estado.
O objetivo de elaboração desta Nota Técnica por meio da aplicação da metodologia escolhida foi avaliar a efetividade das medidas de isolamento impostas pelo município de Maringá (PR) no dia 20 de março de 2020 para combater a epidemia do coronavírus (COVID-19). As medidas foram tomadas a fim de desacelerar a dinâmica do surto e garantir o tratamento hospitalar para a população.
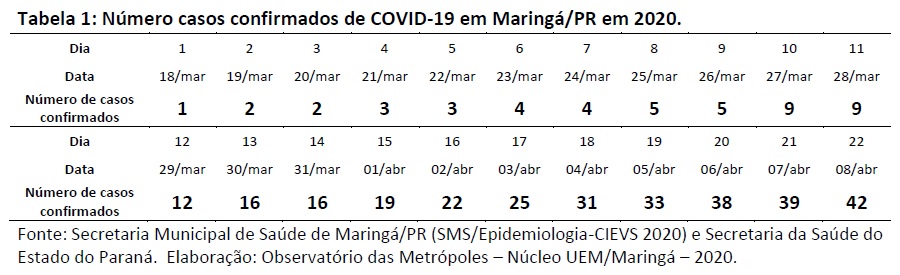
Para as análises, foi utilizado o número de casos confirmados de COVID-19 por dia no município desde o dia 18/03/2020 (data da primeira confirmação) até dia 08 de abril, ou seja, 22 observações (Tabela 1).
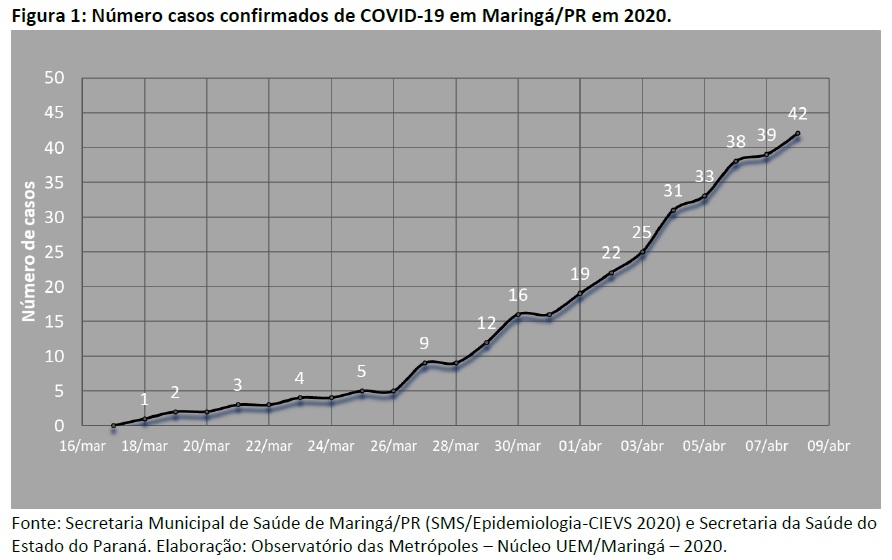
A Figura 1 evidencia o número crescente de casos confirmados em Maringá desde o surgimento do primeiro caso no município.
O modelo matemático utilizado nesta análise é o SIR (Suscetíveis -Infectados- Recuperados). A ideia para a previsão é de que existem três grupos de pessoas: aquelas que são saudáveis, mas suscetíveis à doença (S), as infectadas (I) e as pessoas que se recuperaram (R). É importante destacar algumas suposições necessárias para a utilização deste modelo, entre elas, a de que a população é fechada, isto é, o tamanho da população não muda ao longo do tempo de estudo. Também supomos que, uma vez que um indivíduo infectado é recuperado, ele não ficará doente novamente. Neste sentido, na Figura 2 é apresentada a dinâmica de contaminação do modelo SIR, na qual um indivíduo saudável (suscetível) pode se contaminar (infectado) e após certo tempo se recuperar. Matematicamente, esta dinâmica é modelada em função do tempo através de um sistema de equações diferenciais. Para mais detalhes, ver Kermack e McKendrick (1927) e Michael Höhle (2020).
Para a melhor previsão dos resultados, seriam necessárias as informações de pessoas atualmente infectadas (menos as recuperadas ou mortas), mas o número de pessoas recuperadas por dia não está disponível. Contudo, por ainda estarmos nos estágios iniciais de transmissão não existem muitas recuperações e a influência de tais informações nos resultados é mínima.
A Organização Mundial da Saúde (OMS) informa que a taxa média de transmissão da doença é de 2,25. Esse número representa a quantidade média de pessoas saudáveis que são infectadas por uma pessoa doente e foi utilizado para simular as previsões dos casos confirmados sem as medidas de isolamento social.
Utilizando o número de casos confirmados em Maringá (dados da Tabela 1), o valor estimado para a taxa média de transmissão, a partir da implantação das medidas de isolamento foi de 1,34. Para a obtenção desses resultados foi utilizando o software R (R Core Team, 2019). O valor de 1,34 é inferior ao divulgado pela OMS, indicando que as medidas de isolamento diminuem a taxa média de transmissão do coronavírus e, consequentemente, diminuem a quantidade de pessoas doentes por dia e total, como apresentado a seguir.
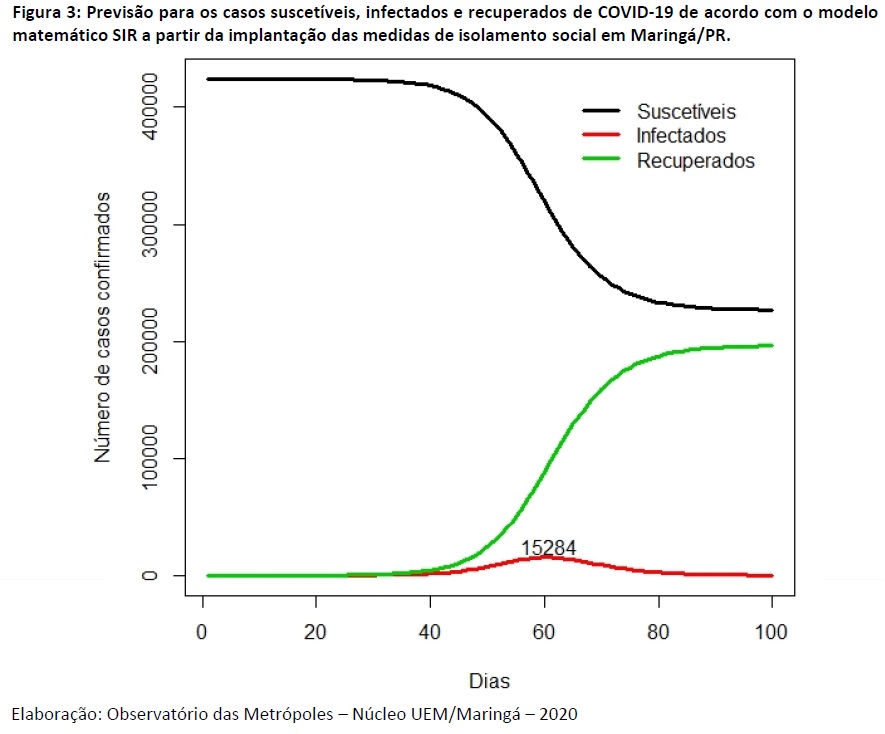
A Figura 3 representa a previsão para 100 dias (iniciando em 18 de março) da dinâmica dos casos suscetíveis, infectados e recuperados segundo o modelo matemático SIR a partir da implantação das medidas de isolamento para Maringá. De acordo com essa previsão, o número máximo de casos confirmados em um dia é 15.284, o que ocorreria em 17 de maio de 2020, 61 dias após a primeira confirmação.
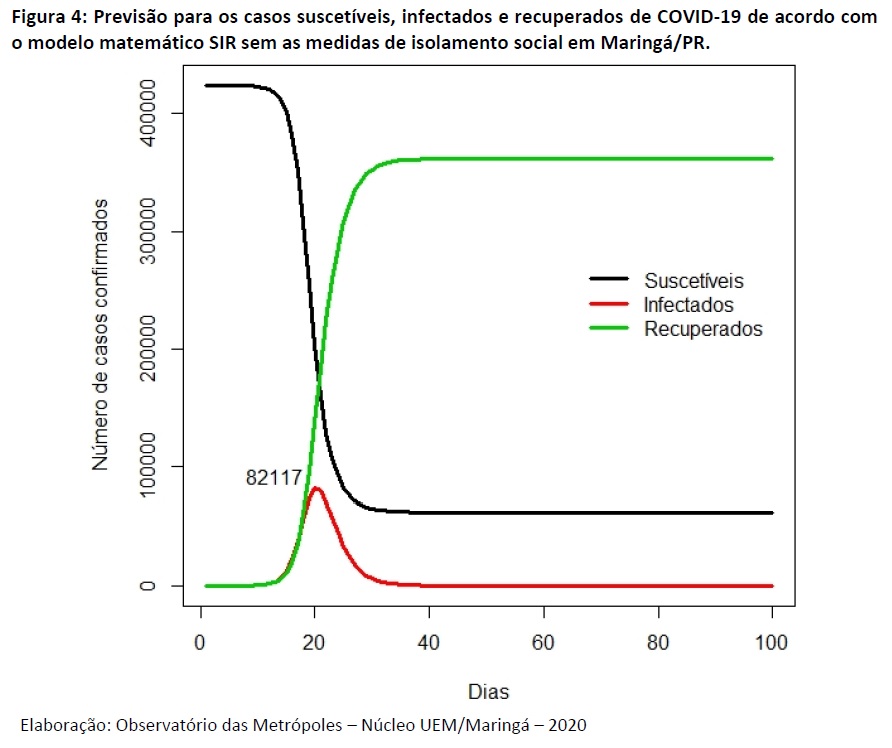
Já a Figura 4 representa a previsão para 100 dias (a partir de 18 de março) caso não tivessem sido tomadas as medidas de isolamento em Maringá, utilizando a taxa média de transmissão de 2,25, divulgada pela OMS. Neste cenário, o número máximo de casos ocorreria no dia 04 de abril de 2020, 20 dias após a primeira confirmação com 82.117 pessoas infectadas neste dia.
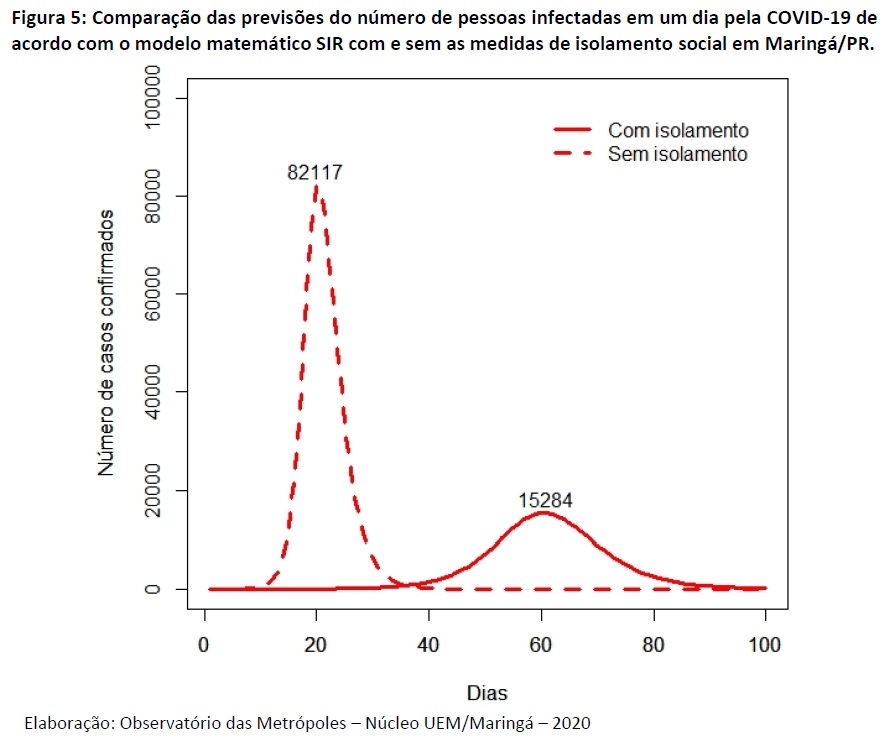
A Figura 5 apresenta a previsão para o número de pessoas infectadas em um dia no período de 100 dias, com base nos casos confirmados de COVID-19 em Maringá. Observa-se a comparação entre o número de casos confirmados de coronavírus com e sem as medidas de isolamento impostas pelo município.
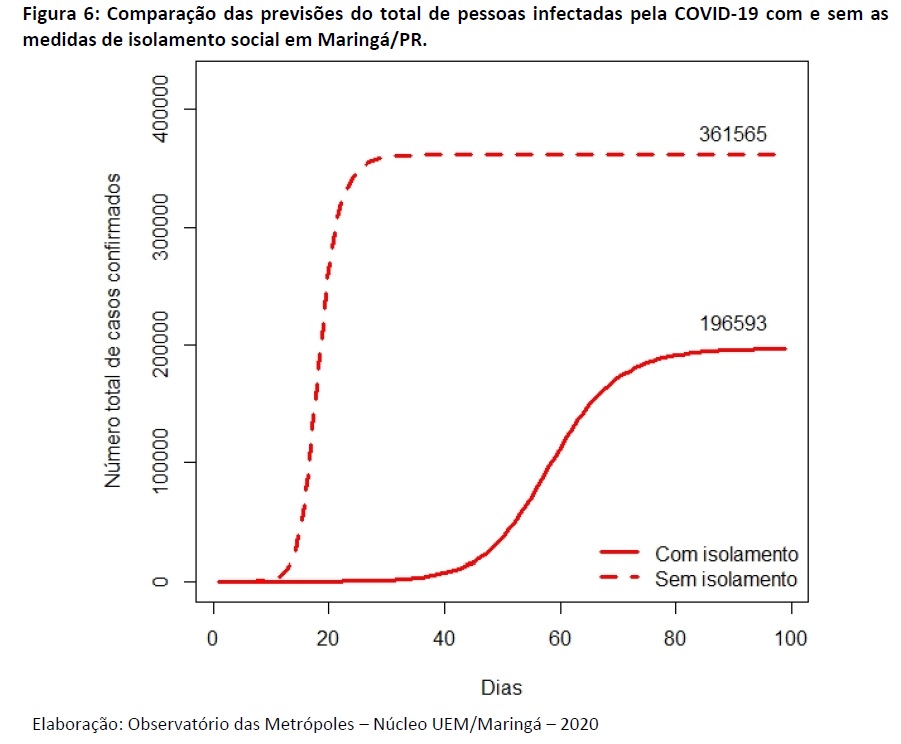
Na Figura 6 tem-se a previsão para a quantidade total de pessoas infectadas no período de 100 dias com e sem as medidas de isolamento social. Com a medida de isolamento a previsão é que, ao final de 100 dias, 196.593 pessoas estariam infectadas, enquanto que sem o isolamento este número sobe para 361.565.
Considerações finais
Por meio dos resultados apresentados, verificou-se que as medidas de isolamento impostas pelo município de Maringá foram efetivas no combate à disseminação de COVID-19, já que com o resultado da simulação pelo modelo matemático SIR observou-se o “achatamento” da curva de infecção, o que resulta em tempo maior para a tomada de medidas como disponibilidade de leitos hospitalares. Além disso, o número máximo de infecções em um único dia é muito menor com as medidas de isolamento, o que evita a sobrecarga do sistema de saúde.
Ao final do período de transmissão, a quantidade total de pessoas infectadas é maior quando não consideramos as medidas de isolamento, portanto e efetividade de tais medidas se confirma. Como limitação deste trabalho é importante destacar, além das suposições apresentadas no início, que as análises apresentadas são preliminares devido à ausência de informações diárias de pacientes recuperados e o fato de estarmos no início do processo de transmissão.
Destacamos que os modelos matemáticos são divergentes, mas todos convergem ao concluir que o total da população a ser afetada é espantoso, como os números apresentados nesta análise de Maringá, absolutamente assustadores. Mas, ressalva-se a informação frequentemente veiculada de que “do total de infectados, 80% não irão desenvolver a doença”, o que se apresenta como uma amenidade diante dos assombrosos dados objetivos.
____________________________________________________________________
¹ Coordenadora do Observatório das Metrópoles Núcleo Maringá.
² Pesquisadora do Observatório das Metrópoles Núcleo Maringá.
³ Pesquisador do Observatório das Metrópoles Núcleo Maringá.
REFERÊNCIAS
CHURCHES. Tim Churches Health Data Science Blog: Modelling the effects of public health interventions on COVID-19 transmission using R – part 1. 2020, March 10. Disponível em: https://timchurches.github.io/blog/posts/2020-03-10-modelling-the-effects-of-public-health-interventions-on-covid-19-transmission-part-1/. Acesso em 05 de abril de 2020.
CONGREGAÇÃO DA FACULDADE DE SAÚDE PÚBLICA DA USP (2020). 27 de março de 2020. Disponível em: https://www.fsp.usp.br/site/noticias/mostra/19357. Acesso em 30 de março de 2020.
CORREIA, Sergio; LUCK, Stephan; VERNER, Emil (2020). As pandemias deprimem a economia, as intervenções de saúde pública não: evidências da gripe de 1918, in SSRN. Disponível em: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3561560. Acesso em 31 de março de 2020.
HÖHLE, Michael. Theory meets practice…: Flatten the COVID-19 curve. Mar 16, 2020. Disponível em: https://staff.math.su.se/hoehle/blog/2020/03/16/flatteningthecurve.html. Acesso em 05 de abril de 2020.
JENNESS S.M.; GOODREAU, S.M.; MORRIS, M. EpiModel: An R Package for Mathematical Modeling of Infectious Disease over Networks. Journal of Statistical Software. 2018; 84(8): 1-47. DOI: 10.18637/jss.v084.i08.
KERMACK, W. O.; MCKENDRICK, A. G.(1927). A Contribution to the Mathematical Theory of Epidemics. Proceedings of the Royal Society, Series A 115: 700–721.
R CORE TEAM (2019). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. Disponível em: https://www.R-project.org/
SASAKI, Kai. The First Cry of Atom: COVID-19 dynamics with SIR model. Disponível em: https://www.lewuathe.com/covid-19-dynamics-with-sir-model.html. Acesso em 05 de abril de 2020.
SOETAERT, Karline; PETZOLDT, Thomas; Setzer, R. Woodrow. Solving Differential Equations in R: Package deSolve. Journal of Statistical Software, 2010, 33(9), 1–25. DOI 10.18637/jss.v033.i09. Disponível em: http://www.jstatsoft.org/v33/i09/